GEOMETRI
Geometri (Yunani Kuno: γεωμετρία, geo-"bumi",-metron "pengukuran") adalah cabang matematika yang bersangkutan dengan pertanyaan bentuk, ukuran, posisi relatif tokoh, dan sifat ruang.
Seorang ahli matematika yang bekerja di bidang geometri disebut ahli
ilmu ukur. Geometri muncul secara independen di sejumlah budaya awal
sebagai ilmu pengetahuan praktis tentang panjang, luas, dan volume, dengan unsur-unsur dari ilmu matematika formal yang muncul di Barat sedini Thales (abad 6 SM). Pada abad ke-3 SM geometri dimasukkan ke dalam bentuk aksiomatik oleh Euclid, yang dibantu oleh geometri Euclid, menjadi standar selama berabad-abad. Archimedes mengembangkan teknik cerdik untuk menghitung luas dan volume, dalam banyak cara mengantisipasi kalkulus integral yang modern. Bidang astronomi,
terutama memetakan posisi bintang dan planet pada falak dan
menggambarkan hubungan antara gerakan benda langit, menjabat sebagai
sumber penting masalah geometrik selama satu berikutnya dan setengah
milenium. Kedua geometri dan astronomi dianggap di dunia klasik untuk
menjadi bagian dari Quadrivium tersebut, subset dari tujuh seni liberal dianggap penting untuk warga negara bebas untuk menguasai.
Pengenalan koordinat oleh René Descartes dan perkembangan bersamaan aljabar menandai tahap baru untuk geometri, karena tokoh geometris, seperti kurva pesawat,
sekarang bisa diwakili analitis, yakni dengan fungsi dan persamaan. Hal
ini memainkan peran penting dalam munculnya kalkulus pada abad ke-17.
Selanjutnya, teori perspektif menunjukkan bahwa ada lebih banyak
geometri dari sekadar sifat metrik angka: perspektif adalah asal
geometri proyektif. Subyek geometri selanjutnya diperkaya oleh studi
struktur intrinsik benda geometris yang berasal dengan Euler dan Gauss dan menyebabkan penciptaan topologi dan geometri diferensial.
Dalam waktu Euclid tidak ada perbedaan yang jelas antara ruang fisik
dan ruang geometris. Sejak penemuan abad ke-19 geometri non-Euclid,
konsep ruang telah mengalami transformasi radikal, dan muncul
pertanyaan: mana ruang geometris paling sesuai dengan ruang fisik?
Dengan meningkatnya matematika formal dalam abad ke-20, juga 'ruang'
(dan 'titik', 'garis', 'bidang') kehilangan isi intuitif, jadi hari ini
kita harus membedakan antara ruang fisik, ruang geometris (di mana '
ruang ',' titik 'dll masih memiliki arti intuitif mereka) dan ruang
abstrak. Geometri kontemporer menganggap manifold, ruang yang jauh lebih
abstrak dari ruang Euclid akrab, yang mereka hanya sekitar menyerupai
pada skala kecil. Ruang ini mungkin diberkahi dengan struktur tambahan,
yang memungkinkan seseorang untuk berbicara tentang panjang. Geometri
modern memiliki ikatan yang kuat dengan beberapa fisika, dicontohkan
oleh hubungan antara geometri pseudo-Riemann dan relativitas umum. Salah
satu teori fisika termuda, teori string, juga sangat geometris dalam
rasa.
Sedangkan sifat visual geometri awalnya membuatnya lebih mudah
diakses daripada bagian lain dari matematika, seperti aljabar atau teori
bilangan, bahasa geometrik juga digunakan dalam konteks yang jauh dari
tradisional, asal Euclidean nya (misalnya, dalam geometri fraktal dan
geometri aljabar)
Materi Geometri :
GEOMETRI
![GEOMETRI]() Reviewed by Rahman
on
8:30 PM
Rating:
Reviewed by Rahman
on
8:30 PM
Rating:



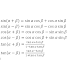


No comments